The arrival of publicly available fast.ai deep learning library is great news for many reasons; cutting edge tools as convenient as possible. USF and International Fellowship students are already learning how powerful this new framework is.
Something remarkable is that a good part of the techniques are so new that there’s lots of room for understanding them better. Even if it is empirically demonstrated their efficiency the rationale behind them is something we can still think about. It seems to me that deeper understanding will make us also better practitioners.
In this post I will focus on a technique introduced in lesson 2 of fast.ai library for the Amazon Planet Kaggle competition. The technique consists in the progressive, sequential resizing of all images while training the convnet, from smaller to bigger sizes.
Obvious? Think twice. Why should this work better than choosing an only optimal size? What makes this different from zoomed images product of image augmentation?
More generally, what does “scale” mean for a convolutional network? Of quite a few conversations with other ML practitioners I infer this is not a well understood topic. Most of us are just happy repeating to ourselves that CNNs are resilient to scale changes, that they learn patterns even if scale changes. But do we really understand how or to what extent scale “doesn’t matter”?
I have to give a little warning; this post, even if not including heavy math formulas is slightly advanced at an abstract level. I assume some familiarity with what a CNN is, how kernels work and what pooling does. If not I recommend to go through the basics on Convolutional Neural Networks and then come back to think about how size of things influence learning of CNNs.
So, what is this “scale invariance” about? I will introduce the topic by asking some simple questions. Suppose you train a CNN with images containing this kitten face, this size and only this size, in different parts of the image, like this:
Now, prediction time, you have this image, much bigger than any other seen during training:
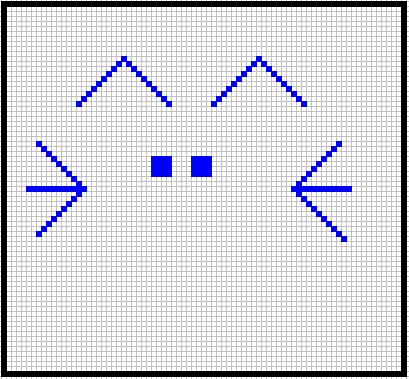
What do you think? Will the network be able to detect the zoomed cat?
What about the opposite, training with much bigger sizes and predicting on smaller sizes?
Notice that in this cat there are two kind of patterns essentially different. The ears and the wiskers are self similar, something typical of fractals (you can cut the ear and the top of it still contains an ear, the “earnes” of that pattern is present as long as the first few pixels of the tip are present). But the eyes are not self similar. If you scale the eyes the pattern black pixel- empty pixel – black pixel is lost. If this “eyes” pattern was learnt in the small version it will not be detected in a bigger version. This pattern is not scale invariant. You can see clearly this self similar patterns highlighted in the next picture:
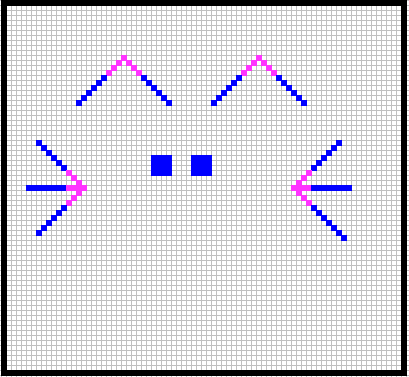
So, one first important understanding is not all features are scale invariant. It should also be clear that scale invariance is a property of (some) of the features, not of the network. The implications are that recognition of a pattern that is not scale invariant can only be made at the same scale it was learnt.
That sounds like horrible news. Does it mean the necessity of exacly matching size of images for recognition of this non invariant patterns? Luckily for us, reality is not that bad: enter pooling concept.
It is known that max-pooling has many virtues, the main one being that it makes a convnet able to detect a previously learnt pattern in a region bigger (and different) than the original specific location of that pattern. It’s quite obvious that compounding of pooling layers gives a CNN the capacity to learn patterns with resilience to translation; no matter where the pattern appears it will be detected.
Less obvious but also true is how this also means scale variation resilience, but only true for self similar patterns: As long as a pattern is detected in the smallest size it can “travel” throughout the layers and its presence detected in the picture.
Lets “converge” back to our original question: Why should using different sizes during training give better performance than just picking the “proper” size from the beginning? Aren’t convnets indiferent to scale variations? And why not achieve this through image augmentation?
About image augmentation, its main use is to increase the number of images adding variety but if the net is to learn systematically about scale dependent patterns all images should be available to it scaled to the same proportion unlike usual image augmentation is done.
The most important question is, of course, why should progresive resizing work. There might be more reasons (I will never understimate the power of a Neural Net to surprise me) but after realizing that images contain scale-dependent patterns I think the answer is more clear.
A CNN will only learn this scale-dependent patterns at a specific combination of size of image and net architecture. This suggests that a variety of ensembling approaches combining image sizes could improve performance. Once assumed this, fast.ai approach of letting the training stage “learn” how to do this ensemble of different scale-dependent information is both straighforward and efficient.